One of the most common thing you can do in Microsoft Excel is to compute the percentage change between 2 numbers. In this tutorial, we'll see exactly how to do that.
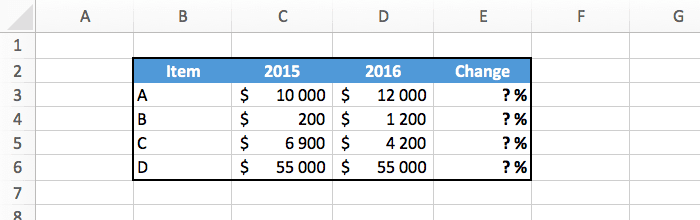
You can see below the data we'll work with. The plan is to fill the last column with the correct percentages and some cool formatting.
Let's start with a tiny bit of math. How do we actually compute the change between 2 numbers? It looks like this:
change = (finalValue - initialValue) / initialValue
We can check if this works with a simple example. If we go from $100 to $150, we get: (150-100)/100 = 50/100 = +50%. So it's fine :-)
I recommend you to learn this formula by heart if that's not already the case, because it is so useful when analyzing data.
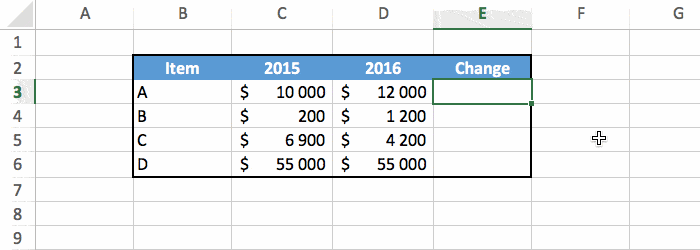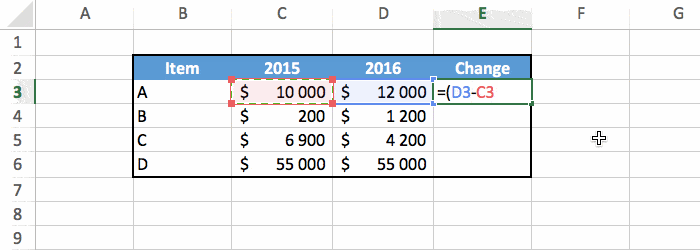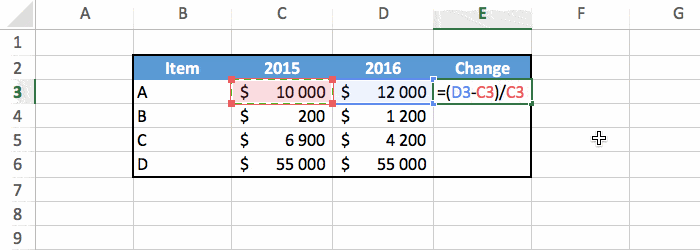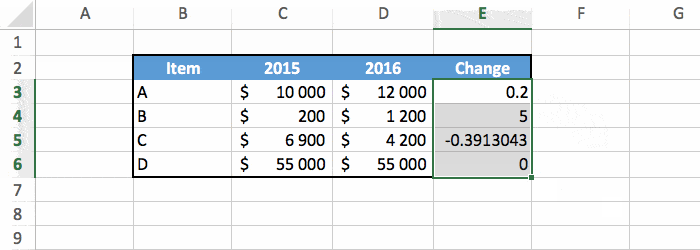
Once you know the math, you just have to write the formula in Excel. Here's the example that you saw at the top of this tutorial.
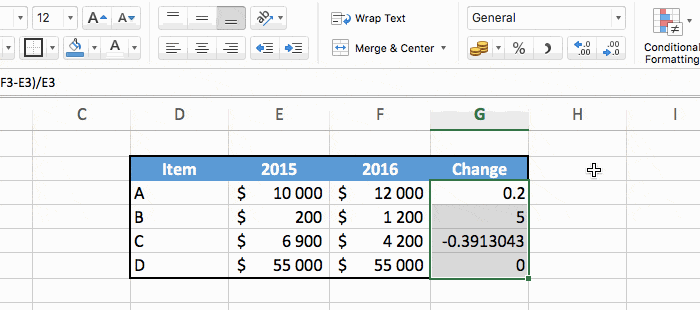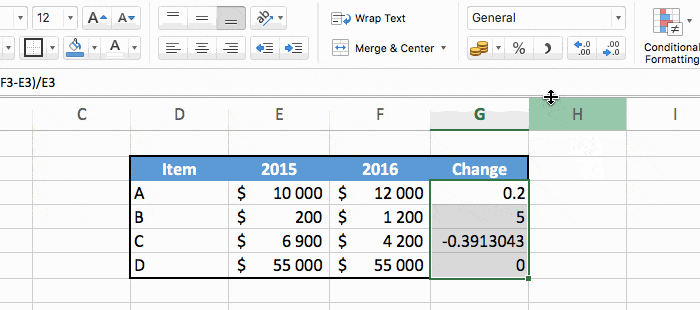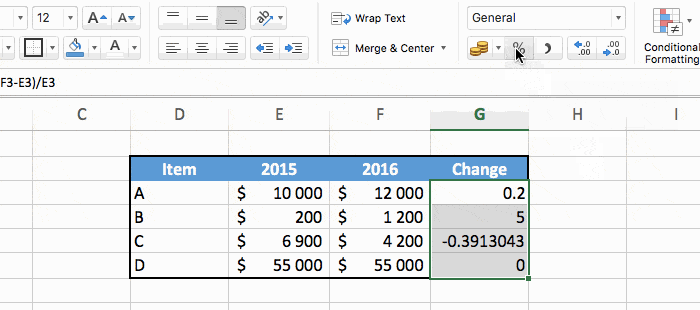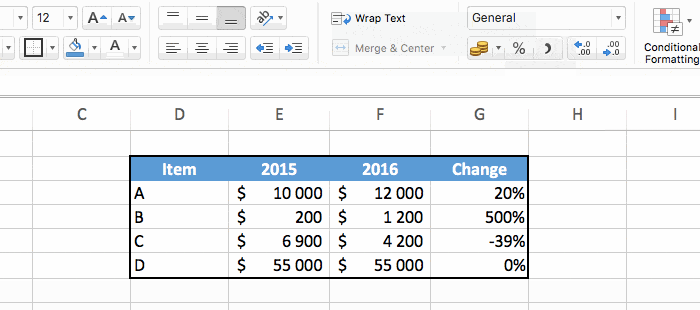
In this case, for the first row of the table we have:
=(D3-C3)/C3 (+20%).So type the formula in the correct cell, and use the fill handle to copy the formula in every row.
And there you have the percentage change for all our values!
We can make things look better with a little formatting.
The simple solution is to just select the cells and set the format to percentage.
It works fine, but we can do better as explained below. Note that this is completely optional.
Select the cells and right click to do "format cells". In the window that appears click on "custom" in the left menu at the very bottom.
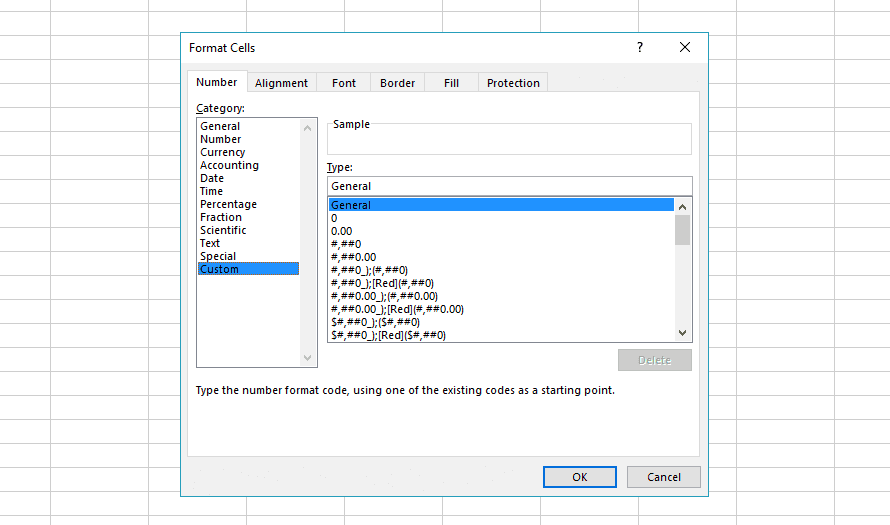
And past this in the "type" field at the top: [Green]+ 0%; [Red]- 0%; 0%
You don't need to understand how this code works, but if you are curious I'll explain this in the "bonus" section below.
Then press enter, and you should see this cool looking result:
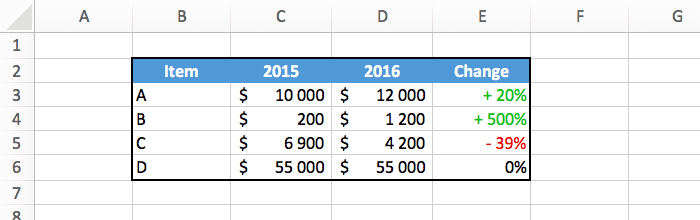
For those of you who want to know how [Green]+ 0%; [Red]- 0%; 0% works, here's your explanation.
The code is actually in three parts, divided by the semicolon character:
[Green]+ 0%. This is used when the number is positive. We set the color to green, add a "+" sign, and display the number with a "%" symbol.[Red]- 0%. This is used when the number is negative. It's similar as above, except that the color is red, and the sign is "-" instead of "+".0%. This is used when the number is exactly zero. This time no colors and no signs, just the number with "%" is displayed.This is a really powerful way to display numbers, but it can become quite complex because it's not really intuitive to use.
As I said earlier, computing the percentage change between 2 numbers is something important that you should know. You just need to remember the formula to compute the change:
change = (finalValue - initialValue) / initialValue
Then it's up to you to add some nice formatting!